Programación numérica + Graficacion.Lanzamiento de proyectiles (Física y Dinámica)

TIRO PARABÓLICO

El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.

En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:

Ø  Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.

Ø  La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.

Ø  Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.

Ø  Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola.

Para el movimiento de proyectiles supondremos que la aceleración es constante y dirigida hacia abajo, además despreciaremos la resistencia del aire.

Las ecuaciones del movimiento de un proyectil en cualquier tiempo son:

v_x = v_x0 = v₀ cos q₀ = const.

v_y =  v_y0 - gt = v₀ sen q₀ - gt

x = v_x0t = v₀ (cos q₀ )t

y =  v_y0t - ½gt² = v₀ (sen q₀)t - ½ gt²

DONDE:

Vx=velocidad en x

Vy = velocidad en y

Vx0=Vy0=Velocidad inicial

q₀ =angulo

X=movimiento en x (desplazamiento)

Y=movimiento en y (altura)

Método de bisección

Este es uno de los métodos más sencillos y de fácil intuición para resolver ecuaciones en una variable. Se basa en el teorema del valor intermedio (TVI), el cual establece que toda función continua f en un intervalo cerrado [a,b] toma todos los valores que se hallan entre f(a) y f(b). Esto es que todo valor entre f(a) y f(b) es la imagen de al menos un valor en el intervalo [a,b]. En caso de que f(a) y f(b) tengan signos opuestos, el valor cero sería un valor intermedio entre f(a) y f(b), por lo que con certeza existe un p en [a,b] que cumple f(p)=0. De esta forma, se asegura la existencia de al menos una solución de la ecuación f(a)=0.

El método consiste en lo siguiente:

Debe existir seguridad sobre la continuidad de la función f(x) en el intervalo [a,b]

A continuación se verifica que

Se calcula el punto medio m del intervalo [a,b] y se evalúa f(m) si ese valor es igual a cero, ya hemos encontrado la raíz buscada

En caso de que no lo sea, verificamos si f(m) tiene signo opuesto con f(a) o con f(b)

Se redefine el intervalo [a, b] como [a, m] ó [m, b] según se haya determinado en cuál de estos intervalos ocurre un cambio de signo

Con este nuevo intervalo se continúa sucesivamente encerrando la solución en un intervalo cada vez más pequeño, hasta alcanzar la precisión deseada

En la siguiente figura se ilustra el procedimiento descrito.

El método de bisección es menos eficiente que el método de Newton, pero es mucho más seguro para garantizar la convergencia. Si f es una función continua en el intervalo [a, b] y f(a)f(b) < 0, entonces este método converge a la raíz de f.

Algoritmo

Leer a (Limite inferior)

Leer b (Limite superior)

Leer tol (tolerancia)

Leer n (numero de iteraciones)

i=1

Mientras  i <= n

   r = (a+b)/2

   Si |f(r)| <= tol

      Romper ciclo

   Sino

     Si f(a)*f(b) > 0

        a = r

     Sino

        b = r

     Fin   

   Fin

    i = i + 1

Fin

Si i>n

  Escribe(“No se encontró solucion”)

Sino

Escribe(“Solucion encontrada aprox=”, r)

Este método se aplicara a un situación real en este caso lanzamiento de pelotas.

Programa en C++ del tiro parabólico

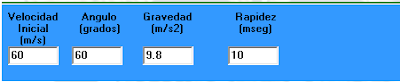
Interfaz Grafica

Parámetros para el cálculo de las incógnitas

Parámetros para el cálculo de la altura máxima con el método de bisección.

Simulación

Tabla de valores en cada iteración y grafica

Código donde se implementa el método de bisección

float ymax, tm;

    Panel1->Enabled=false;

    x=vo*cos(grados)*tiempo;

    y=vo*sin(grados)*tiempo-(.5*gravedad*(tiempo*tiempo));  //1/2*tiempo

    vy= vo* sin(grados) - (gravedad*tiempo);

    tiempo+=0.1;

   if (y<0)

    {

      tm=vo*sin(grados)/gravedad;

      ymax=(gravedad*tm*tm)/2;

      _ymax=ymax;

      N = Edit8->Text.ToInt();

      R = Biseccion(N, 0.01, 0.0, ymax);

Label1->Caption="La pelota cayo en " + FloatToStr(tiempo)  + " seg. A una distancia de: " + FloatToStr (x) + " mts. Su altura maxima fue: " + FloatToStr(R);

      Panel1->Enabled=true;

      Timer1->Enabled=false;

      PaintBox1->Invalidate();

    }

El usuario da el máximo de iteraciones, la tolerancia y el intervalo de definen por el programador

Uso del método del bisección en el programa para calcular la altura máxima

double TForm1::Biseccion(int n, double tol, double a, double b)

{

    int i = 1;

    double r;// = (a + b)/2;

    while(i < n )

    {

       r = (a + b) / 2;

       if(f(r) <= tol)

         break;

       else

       {

       if((f(a) * f(r)) >= 0)

          a = r;

       else

          b = r;

       }

       i++;

      

    }

    return r;//La raiz es r

}

//----------------------------------------------------------------

FUNCION ALTURA MAXIMA

double TForm1::f(double x)

{

double val = (gravedad/0.01 + (vo*sin(grados)))*x/(vo*cos(grados))+gravedad*log(1.0-x*0.01/(vo*cos(grados)))/(0.01*0.01);

    return val;

}

CONCUSION

El aplicar métodos numéricos es muy sencillo cuando se trata de ecuaciones encillas que calculan o solucionan  algún problema de la vida cotidiana como lo es el calcular el alcance máximo o la altura máxima.

Para el método de bisección la ecuación que use que muy bien y arroja un buen resultado ya que el intervalo se da de manera que encierra a la raíz pero se llega a la solución después de un numero grande de iteraciones.

La razón por la que escogimos esta ecuación es porque nos daba un acercamiento similar a otros métodos aunque usaba más iteraciones no las iteraciones que usaba.

La diferencia de iteraciones no era mucha asi que decidimos usar este método.

Código completo

    int x,y;

    float vy;

    float vo=30;

    float tiempo=0;

    float grados=60*M_PI/180;

    float gravedad=9.8;

    int espera=60;

//---------------------------------------------------------------------------

__fastcall TForm1::TForm1(TComponent* Owner)

        : TForm(Owner)

{

}

//---------------------------------------------------------------------------

 int i=0;

 int tam=4;

 int _ymax;

void __fastcall TForm1::Timer1Timer(TObject *Sender)

{

    float ymax, tm;

    Panel1->Enabled=false;

    x=vo*cos(grados)*tiempo;

    y=vo*sin(grados)*tiempo-(.5*gravedad*(tiempo*tiempo));  //1/2*tiempo

    vy= vo* sin(grados) - (gravedad*tiempo);

    tiempo+=0.1;

   if (y<0)

    {

      tm=vo*sin(grados)/gravedad;

      ymax=(gravedad*tm*tm)/2;

      _ymax=ymax;

      N = Edit8->Text.ToInt();

      R = Biseccion(N, 0.01, 0.0, ymax);

      Label1->Caption="La pelota cayo en " + FloatToStr(tiempo)  + " seg. A una distancia de: " + FloatToStr (x) + " mts. Su altura maxima fue: " + FloatToStr(R);

      Panel1->Enabled=true;

      Timer1->Enabled=false;

      PaintBox1->Invalidate();

    }

   if (y>PaintBox1->Height)

    {

      Label1->Caption="La bala ha salido de la pantalla";

       if (tiempo>espera)

        {

            Label1->Caption="La pelota no ha caido en " + FloatToStr (tiempo+espera) + " segundos.";

            Panel1->Enabled=true;

            Timer1->Enabled=false;

        }

    }

    StringGrid1->Cells[0][i+1]= i+1;   //

    StringGrid1->Cells[1][i+1]= double(int(tiempo*100.0+.5))/100.0;

    StringGrid1->Cells[2][i+1]= x;

    StringGrid1->Cells[3][i+1]= y;

    StringGrid1->Cells[4][i+1]= vo;

    StringGrid1->Cells[5][i+1]= double(int(vy*100.0+.5))/100.0;

    i++;

    StringGrid1->RowCount=tam++;

    PaintBox1->Invalidate();

}

//---------------------------------------------------------------------------

void __fastcall TForm1::PaintBox1Paint(TObject *Sender)

{

   SetMapMode (PaintBox1->Canvas->Handle, MM_ANISOTROPIC);

   SetWindowExtEx(PaintBox1->Canvas->Handle, PaintBox1->Width, PaintBox1->Height,NULL);

   SetViewportExtEx(PaintBox1->Canvas->Handle, PaintBox1->Width,  -PaintBox1->Height, NULL);

   SetViewportOrgEx(PaintBox1->Canvas->Handle,0,PaintBox1->Height,NULL);

   PaintBox1->Canvas->Brush->Color=clSkyBlue;

   PaintBox1->Canvas->Ellipse(x,y,x+20,y+20);

}

//---------------------------------------------------------------------------

void __fastcall TForm1::PaintBox1Click(TObject *Sender)

{

    Invalidate();

}

//---------------------------------------------------------------------------

void __fastcall TForm1::BitBtn1Click(TObject *Sender)

{

   Timer1->Enabled=true;

   tiempo=0;

   Label1->Caption="";

   Image2->Visible=false;

   Image3->Visible=true;

}

//---------------------------------------------------------------------------

void __fastcall TForm1::Edit1Exit(TObject *Sender)

{

   vo=StrToFloat (Edit1->Text);     //VELOCIDAD INICIAL

}

//---------------------------------------------------------------------------

void __fastcall TForm1::Edit2Exit(TObject *Sender)

{

  if (StrToFloat (Edit2->Text)>=90)

     ShowMessage ("El angulo no puede ser mayor a 90");

  grados=StrToFloat(Edit2->Text)*M_PI/180;

}

//---------------------------------------------------------------------------

void __fastcall TForm1::Edit4Exit(TObject *Sender)

{

    Timer1->Interval=StrToInt(Edit4->Text);

}

//---------------------------------------------------------------------------

void __fastcall TForm1::Edit3Exit(TObject *Sender)

{

    gravedad=StrToFloat(Edit3->Text);

}

//---------------------------------------------------------------------------

void __fastcall TForm1::Edit5Exit(TObject *Sender)

{

    espera=StrToInt(Edit5->Text);

}

//---------------------------------------------------------------------------

void __fastcall TForm1::FormCreate(TObject *Sender)

{

    Form1->DoubleBuffered=true;

    StringGrid1->ColCount=9;

   // StringGrid1->Rows->Add(1);

   StringGrid1->Cells[0][0]="Iteracion";

   StringGrid1->Cells[1][0]="Tiempo";

   StringGrid1->Cells[2][0]="X";

   StringGrid1->Cells[3][0]="Y";

   StringGrid1->Cells[4][0]="Vx";

   StringGrid1->Cells[5][0]="Vy";

   StringGrid1->Cells[6][0]="h max (r)";

   StringGrid1->Cells[7][0]="f(a)";

   StringGrid1->Cells[8][0]="f(r)";

}

//---------------------------------------------------------------------------

double TForm1::Biseccion(int n, double tol, double a, double b)

{

    int i = 1;

    double r;// = (a + b)/2;

    while(i < n )

    {

     

       r = (a + b) / 2;

       if(f(r) <= tol)

         break;

       else

       {

       if((f(a) * f(r)) >= 0)

          a = r;

       else

          b = r;

       }

       i++;

       StringGrid1->Cells[6][i-1]= double(int(r*100.0+.5))/100.0;

       StringGrid1->Cells[7][i-1]= double(int(f(a)*100.0+.5))/100.0;;

       StringGrid1->Cells[8][i-1]= double(int(f(r)*100.0+.5))/100.0;

    }

    return r;

}

//---------------------------------------------------------------------------

double TForm1::f(double x)

{

    double val = (gravedad/0.01 + (vo* sin(grados)))*x/(vo*cos(grados))+gravedad*log(1.0-x*0.01/(vo*cos(grados)))/(0.01*0.01); //

    return val;

}

bool primer=true;

int xx;

int yy;

void __fastcall TForm1::Timer2Timer(TObject *Sender)

{

   if(primer==true)

    {

      xx=0;

      yy=PaintBox2->Height;

    }

   PaintBox2->Canvas->Pen->Color=clBlue;

   PaintBox2->Canvas->Pen->Width=random(3);

   PaintBox2->Canvas->LineTo(x,yy-y);

  // PaintBox2->Canvas->MoveTo(0,y-0);

   //PaintBox2->Canvas->LineTo(20, y-20);

}

//---------------------------------------------------------------------------

bool primer1=false;

int xxx;

int yyy;

void __fastcall TForm1::Button2Click(TObject *Sender)

{

 if(primer1==true)

    {

      xxx=0;

      yyy=PaintBox2->Height;

     // primer=false;

    }

  for(int i=0; i<=200; i++)

   {

   double val = (gravedad/0.01 + (vo* sin(grados)))*i/(vo*cos(grados))+gravedad*log(1.0-i*0.01/(vo*cos(grados)))/(0.01*0.01);

   PaintBox2->Canvas->Pen->Color=clBlue;

   PaintBox2->Canvas->Pen->Width=3;

   PaintBox2->Canvas->LineTo(i,yyy-val);

   }

}

//--------------------------------------------------------------- 

El programa anterior fue un proyecto para la materia Métodos Numéricos usando métodos iterativos + programación gráfica básica y aplicándolos a sistemas reales que involucran fuerza, velocidad y aceleración.